Eine Möglichkeit, musikalische Harmonie zu sehen

Wenn wir über Melodie sprechen, haben wir einen sehr guten Helfer – die Daube.

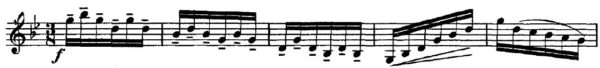
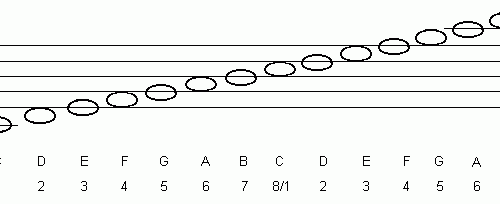
Wenn man sich dieses Bild ansieht, kann sogar eine Person, die mit musikalischer Bildung nicht vertraut ist, leicht feststellen, wann die Melodie ansteigt, wann sie abfällt, wann diese Bewegung glatt ist und wann sie springt. Wir sehen buchstäblich, welche Noten melodisch näher beieinander liegen und welche weiter entfernt sind.

Aber im Bereich der Harmonik scheint alles ganz anders zu sein: geschlossene Töne zum Beispiel, zu и ре klingen ziemlich dissonant zusammen, und entferntere, zum Beispiel, zu и E – viel melodiöser. Zwischen der völlig konsonanten Quarte und Quinte liegt ein völlig dissonanter Tritonus. Die Logik der Harmonie entpuppt sich als irgendwie völlig „nicht-linear“.

Ist es möglich, ein solches visuelles Bild aufzunehmen, anhand dessen wir leicht feststellen können, wie „harmonisch“ zwei Töne nahe beieinander liegen?

 „Valenzen“ des Klangs

Erinnern wir uns noch einmal daran, wie der Ton angeordnet ist (Abb. 1).

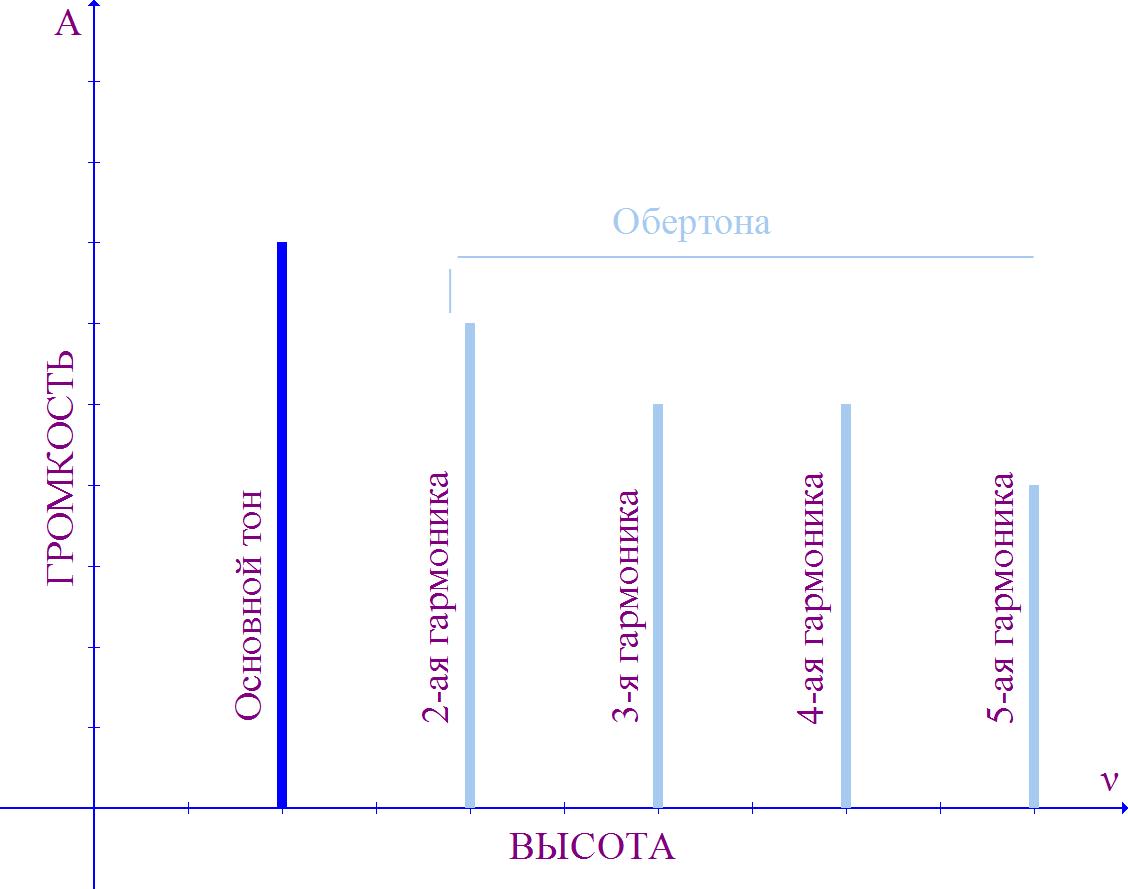
Jede vertikale Linie im Diagramm repräsentiert die Obertöne des Klangs. Alle sind Vielfache des Grundtons, das heißt, ihre Frequenzen sind 2-, 3-, 4-mal (und so weiter) größer als die Frequenz des Grundtons. Jede Harmonische ist eine sogenannte monochromer Klang, das heißt, der Ton, in dem es eine einzige Schwingungsfrequenz gibt.

Wenn wir nur eine Note spielen, erzeugen wir tatsächlich eine große Anzahl monochromer Klänge. Zum Beispiel, wenn eine Note gespielt wird für kleine Oktave, dessen Grundfrequenz 220 Hz beträgt, erklingen gleichzeitig monochromatische Töne mit Frequenzen von 440 Hz, 660 Hz, 880 Hz usw. (etwa 90 Töne im menschlichen Hörbereich).

Wenn wir eine solche Struktur von Obertönen kennen, versuchen wir herauszufinden, wie man zwei Klänge auf einfachste Weise verbindet.

Der erste, einfachste Weg besteht darin, zwei Töne zu nehmen, deren Frequenzen sich genau zweimal unterscheiden. Mal sehen, wie es in Bezug auf Obertöne aussieht, indem man die Töne untereinander platziert (Abb. 2).

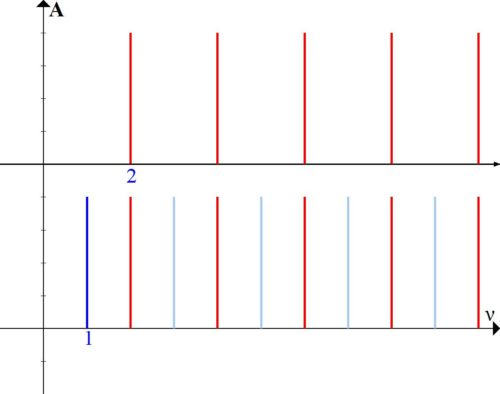
Wir sehen, dass in dieser Kombination die Klänge tatsächlich jede zweite Harmonische haben (übereinstimmende Harmonische sind rot gekennzeichnet). Die beiden Sounds haben viel gemeinsam – 50%. Sie werden „harmonisch“ sehr nahe beieinander liegen.

Die Kombination zweier Töne wird, wie Sie wissen, als Intervall bezeichnet. Das in Abbildung 2 dargestellte Intervall wird aufgerufen Oktave.

Es ist erwähnenswert, dass ein solches Intervall, das mit der Oktave „zusammenfällt“, kein Zufall ist. Tatsächlich war der Prozess historisch natürlich umgekehrt: Zuerst hörten sie, dass zwei solcher Klänge sehr glatt und harmonisch zusammenklangen, legten die Methode fest, ein solches Intervall zu konstruieren, und nannten es dann „Oktave“. Die Bauweise ist primär, der Name sekundär.

Die nächste Art der Kommunikation besteht darin, zwei Töne zu nehmen, deren Frequenzen sich um das Dreifache unterscheiden (Abb. 3).

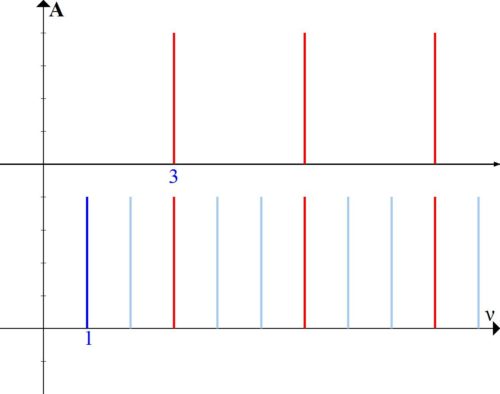
Wir sehen, dass die beiden Klänge hier viel gemeinsam haben – jede dritte Harmonische. Diese beiden Töne werden auch sehr nahe beieinander liegen, und das Intervall wird dementsprechend konsonant sein. Mit der Formel aus der vorherigen Notiz können Sie sogar berechnen, dass das Maß für die Frequenzkonsonanz eines solchen Intervalls 33,3% beträgt.

Dieses Intervall wird aufgerufen Duodezim oder eine Quint bis eine Oktave.

Und schließlich besteht die dritte Art der Kommunikation, die in der modernen Musik verwendet wird, darin, zwei Töne mit einer Chatot-Differenz von 5 Mal zu nehmen (Abb. 4).

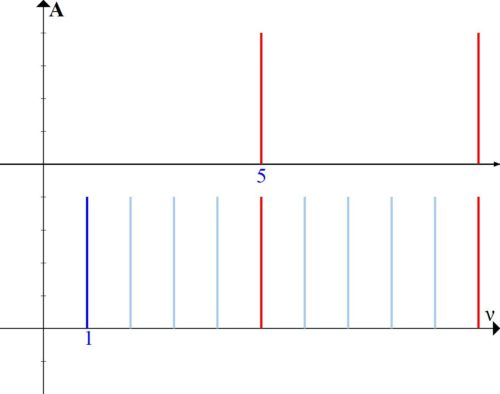
Ein solches Intervall hat nicht einmal einen eigenen Namen, es kann nur als Terz nach zwei Oktaven bezeichnet werden, aber wie wir sehen, hat diese Kombination auch ein ziemlich hohes Maß an Konsonanz – jeder fünfte Oberton fällt zusammen.

Wir haben also drei einfache Verbindungen zwischen Noten – eine Oktave, ein Duodezim und eine Terz bis zwei Oktaven. Wir nennen diese Intervalle einfach. Mal hören, wie sie klingen.

Audio 1. Oktave

.

Audio 2. Duodezima

.

Audio 3. Terz bis Oktave

.

In der Tat ziemlich konsonant. In jedem Intervall besteht der obere Klang tatsächlich aus den Obertönen des unteren und fügt seinem Klang keinen neuen monochromen Klang hinzu. Hören wir uns zum Vergleich an, wie eine Note klingt zu und vier Anmerkungen: zu, ein Oktavton, ein Duodezimalton und ein Ton, der alle zwei Oktaven um ein Drittel höher ist.

Audio 4. Ton zu

.

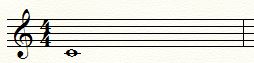
Audio 5. Akkord: CCSE

.

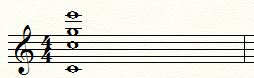
Wie wir hören, ist der Unterschied gering, nur wenige Obertöne des Originalklangs werden „verstärkt“.

Aber zurück zu den Grundintervallen.

Vielfältiger Raum

Wenn wir eine Note auswählen (z. B. zu), dann sind die Noten, die einen Grundschritt davon entfernt sind, am „harmonischsten“ am nächsten dran. Am nächsten wird die Oktave sein, etwas weiter das Duodezimal und dahinter – die dritte bis zwei Oktaven.

Außerdem können wir für jedes Basisintervall mehrere Schritte unternehmen. Wir können zum Beispiel einen Oktavklang bauen und dann einen weiteren Oktavschritt daraus machen. Dazu muss die Frequenz des Originaltons mit 2 multipliziert werden (wir erhalten einen Oktavton) und dann wieder mit 2 multipliziert werden (wir erhalten eine Oktave von einer Oktave). Das Ergebnis ist ein Klang, der 4-mal höher ist als das Original. In der Abbildung sieht es so aus (Abb. 5).

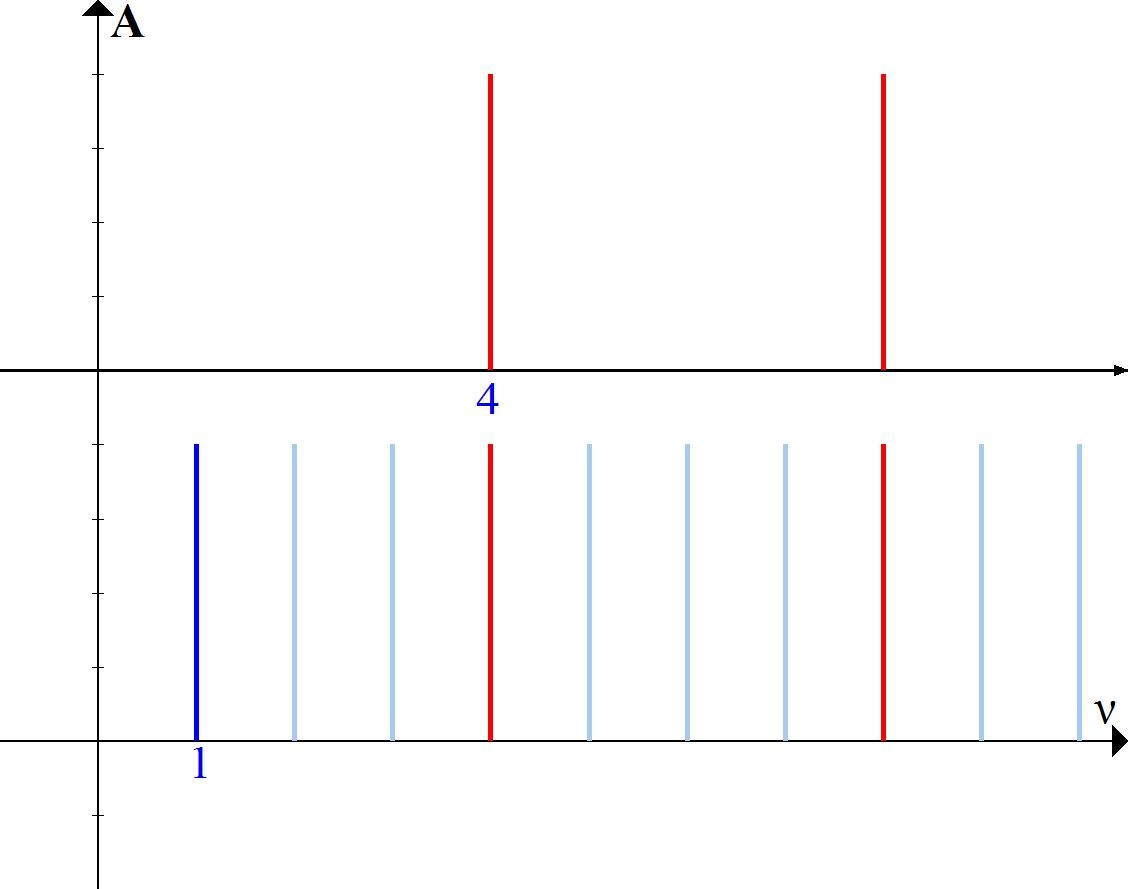
Es ist zu erkennen, dass die Klänge mit jedem weiteren Schritt immer weniger gemeinsam haben. Wir entfernen uns immer weiter von der Konsonanz.

Übrigens werden wir hier analysieren, warum wir die Multiplikation mit 2, 3 und 5 als Basisintervalle genommen und die Multiplikation mit 4 übersprungen haben. Die Multiplikation mit 4 ist kein Basisintervall, weil wir es mit bereits vorhandenen Basisintervallen erhalten können. In diesem Fall entspricht die Multiplikation mit 4 zwei Oktavschritten.

Anders verhält es sich mit Basisintervallen: Es ist unmöglich, sie aus anderen Basisintervallen zu gewinnen. Es ist unmöglich, durch Multiplizieren von 2 und 3 weder die Zahl 5 selbst noch eine ihrer Potenzen zu erhalten. Die Basisintervalle stehen gewissermaßen „senkrecht“ zueinander.

Versuchen wir es uns vorzustellen.

Lassen Sie uns drei senkrechte Achsen zeichnen (Abb. 6). Für jeden von ihnen zeichnen wir die Anzahl der Schritte für jedes Grundintervall auf: auf der zu uns gerichteten Achse die Anzahl der Oktavschritte, auf der horizontalen Achse die Duodezimalschritte und auf der vertikalen Achse die Tertianschritte.

Ein solches Diagramm wird aufgerufen Raum der Vielheiten.

Die Betrachtung des dreidimensionalen Raums in einer Ebene ist ziemlich unbequem, aber wir werden es versuchen.

Auf der Achse, die auf uns gerichtet ist, legen wir Oktaven frei. Da alle Noten, die eine Oktave voneinander entfernt liegen, gleich benannt werden, wird diese Achse für uns am uninteressantsten sein. Aber die Ebene, die von der duodezimalen (fünften) und der tertianischen Achse gebildet wird, werden wir uns genauer ansehen (Abb. 7).

Hier sind die Noten mit Kreuzen gekennzeichnet, ggf. können sie mit Bs als enharmonisch (also klanggleich) bezeichnet werden.

Lassen Sie uns noch einmal wiederholen, wie dieses Flugzeug gebaut wird.

Nachdem wir eine Note ausgewählt haben, einen Schritt rechts davon, platzieren wir die Note, die ein Duodezim höher ist, links – ein Duodezim tiefer. Wenn wir zwei Schritte nach rechts gehen, erhalten wir Duodecyma von Duodecyma. Nehmen Sie zum Beispiel zwei Duodezimalschritte von der Note zu, wir bekommen eine Notiz ре.

Ein Schritt entlang der vertikalen Achse ist eine Terz durch zwei Oktaven. Wenn wir entlang der Achse nach oben gehen, ist dies eine Terz bis zwei Oktaven nach oben, wenn wir nach unten gehen, ist dieses Intervall festgelegt.

Sie können von jeder Note und in jede Richtung gehen.

Mal sehen, wie dieses Schema funktioniert.

Wir wählen eine Note. Schritte machen für Noten erhalten wir eine Note, die immer weniger mit dem Original übereinstimmt. Je weiter die Noten in diesem Raum voneinander entfernt sind, desto weniger konsonante Intervalle bilden sie. Die nächsten Töne sind Nachbarn entlang der Oktavachse (die sozusagen auf uns gerichtet ist), etwas weiter – Nachbarn entlang des Zwölffingerdarms und noch weiter – entlang der Terts.

Zum Beispiel, um von der Notiz zu bekommen zu bis auf eine Note Ihre, müssen wir einen Duodezimalschritt machen (wir erhalten Salz), und dann tert man jeweils das resultierende Intervall do-yes wird weniger konsonant sein als duodecime oder Terz.

Wenn die „Abstände“ im PC gleich sind, dann sind die Konsonanzen der entsprechenden Intervalle gleich. Das einzige, was wir nicht vergessen dürfen, ist die Oktavachse, die unsichtbar in allen Konstruktionen vorhanden ist.

Dieses Diagramm zeigt, wie nahe die Noten „harmonisch“ beieinander liegen. Nach diesem Schema ist es sinnvoll, alle harmonischen Konstruktionen zu betrachten.

Sie können mehr darüber lesen, wie das geht in „Musiksysteme bauen“Nun, darüber reden wir das nächste Mal.

Autor – Roman Oleinikov